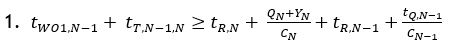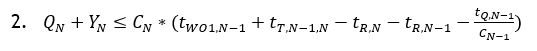Demand-Based Production from a Flow-Time Versus Need-Time Perspective
From a flow-time perspective, Work Orders should arrive in a Work Center's queue at precisely the time when they are needed to be worked on. This minimizes both production cycle-time and inventory investment. The desired time for the next WO to arrive for processing is when the currently-authorized work in a WC and its upstream-adjacent (UA) WCs has been started into the WC and cleared the first operation in the WCs routing. This assumes that demand exists for the WO at the next downstream work cell.
In the figure below, for example, WCs #130 and #135 would both be considered UA for WC #145 (refer to this destination WC as WCN), since work from both of these WCs flows into WC #145. In this construct, WO1 can be considered to be a WO that has not yet been authorized (assigned a Pull-Tag) for processing in its WC (WC #135), and that has the highest priority of any WOs in any WCs that are UA to WC #145. In this case, since WO1 is in WC #135, WC #135 can be referred to as WCN-1. The processing Flow Time, the elapsed time necessary to complete processing, for WO1 in WCN-1 plus its transit time from WCN-1 to WCN should be equal to, and certainly not greater than the time required to completely flush the WOs ahead of it through WCN’s queue and first operation. That is the time that WCN will be ready to begin processing it.
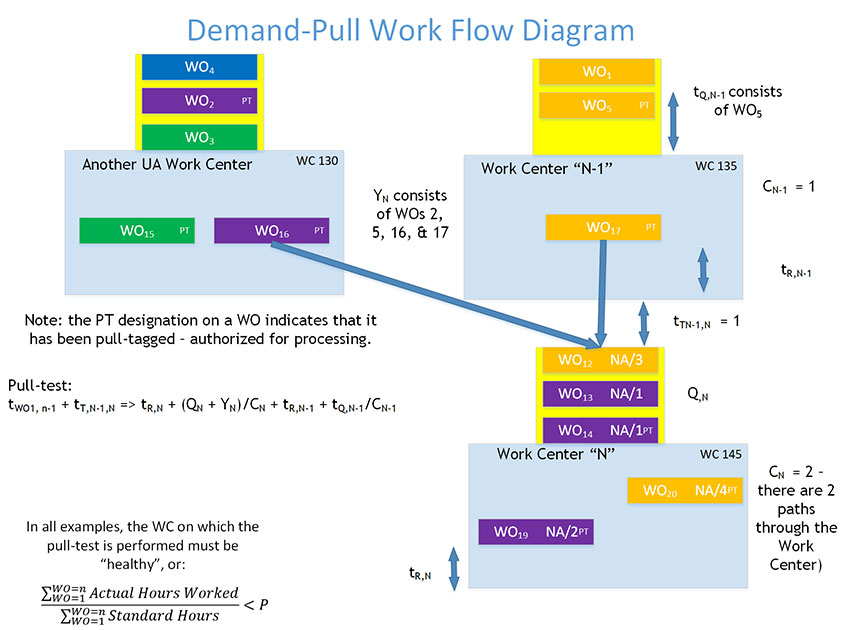
This timing can be modeled as shown in the figure above. WO1 can be assigned a PT when the sum of the Flow Time of WO1 in WCN-1 (tWO1, n-1) plus its transit time from WCN-1 to WCN (tT,N-1,N) [the sum of these two values is the time it takes WO1 to arrive at the WCN queue, once it is started into WCN-1] is equal to or greater than the remaining Flow, Transit, and Clear times of all the previously-authorized WOs ahead of it and destined for WCN or already in the WCN queue.
This latter time can be modeled as the time to process the WO with the least remaining Clear Time in WCN's first operation (tR,N) [this is the elapsed time until the next production start will take place at WCN, thus pulling the next WO from the WCN queue] plus ((the sum of the WCN Clear Times of WOs in the WCN queue (QN) and the sum of the WCN Clear Times for all UA WOs already authorized (YN)), divided by the number of capacity units at WCN (CN) [this is the time it will take to process all upstream and queued WOs through WCN, accounting for the fact that some WCs may have the capacity to simultaneously work on multiple WOs and neglecting the transit time between cell pairs]), plus the remaining Clear Time at the WC in which WO1 resides for the WO with the least remaining Clear Time of all WOs that are in the WCN-1 first operation (tR,N-1) [this is the time it will take for the first, currently in-process, UA WO to complete processing at WCN-1’s first operation and trigger the start of the next WO into WCN-1], plus the quotient of the authorized WCN-1 queue Clear Times (tQ,N-1) and the number of capacity units in WCN-1 (CN-1)) [this is the time required to process all the currently-authorized WCN-1 queue through WCN-1’s first operation and thus the time at which WO1 would be started into the WCN-1 WIP area].
Or when:
Where all variables are specified in the Table of Definitions.
Multiplying through by CN and rearranging to simplify:
When this equality is true, then the next WO (WO1) should be authorized (assigned a Pull-tag). This is what the demand-pull system does by continuously monitoring the state of the factory in the context of the parameters of this equation. Some of these parameters, like the Standard Process Hours that are used to determine the Flow Times that comprise YN, QN, tw01, n-1, and tQ, N-1, come directly from the ERP/MRP system, while other parameters are continuously monitored / calculated by the demand-pull system to complete the algorithm and assign the Pull-Tags as appropriate for the production process.