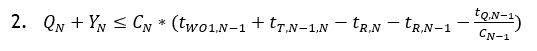high mix manufacturing

 

CalAmp, Inc.

  DEHART CONSULTING, INC.'s flow-based manufacturing methods enabled California Amplifier to significantly reduce floor space, manufacturing cycle-time, and overhead staffing requirements, reduce our material costs by nearly 20%, while over tripling California Amplifier's inventory turns to 10+...  


Fred Sturm, President and CEO California Amplifier, Inc.

An Optimum Queue Policy

The formulae from Demand-Based Production from a Flow-Time Versus Need-Time Perspective and Demand-Based Production from a Work-Volume Perspective can now be combined to solve for the Queue Policy (XN).   From Demand-Based Production from a Work-Volume Perspective, equation 22:

equation 22

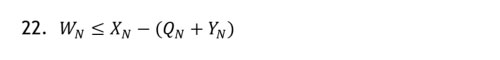
From Demand-Based Production from a Flow-Time Versus Need-Time Perspective, equation 2:

equation 2

Therefore:

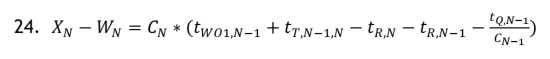
equation 24

and the Queue Policy for WCN is given by:

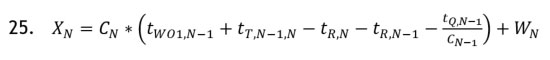
equation 25

From Demand-Based Production from a Work-Volume Perspective, this value of XN can be used to assign a Pull Tag to WO1 when the sum of its Clear Time in WCN (WN) + the queued Clear Times in the WCN queue (QN) + the sum of the Clear Times at WCN for all authorized UA WOs' (YN) is less than or equal to that value of XN. This formula, in the limit where all flow-times are 0, sets a "floor" of WN hours, which is needed to avoid "starving" a WC by setting a maximum Queue Policy that is less than the number of hours represented by the next WO to be authorized. All of the stated terms are "knowable" quantities within the construct of most ERP/MRP systems so that this construct is easily implementable.

    The question can be raised as to why the formula from Demand-Based Production from a Work-Volume Perspective is re-introduced to define a pull algorithm, or why the flow formula (Equation 2 above) cannot just be used to assign Pull tags.  The answer is primarily a matter of visual management in a lean environment. The concept of a maximum Queue Policy is a manageable and understandable concept in the factory environment and one for which the present technology provides management over-rides and/or adjustment factors to accommodate the realities of variability in the individual WCs.  This pull-system conforms to the idea that when inventory falls below a pre-determined policy level, a replenishment signal is sent, yet at the same time, by using ideal flow times, it is forcing queued inventory toward zero.

  • DCI Introduces Vortex Demand-Pull Technology +

    Since the early 1980's, the benefits of producing a given production volume throughput with the minimum amount of inventory have been well documented.  Beginning with the Just-in-Time methodologies, using Kanban cards for inventory replenishment, to Demand Flow methodologies,



    Read more
  • Vortex Introduction +

    The time-based demand-pull system (“demand-pull system”) technology of the described demand-pull system provides an implementation of demand-pull scheduling for various production operations/systems/factories.  It works in conjunction with a Material Resource Planning (MRP) or Enterprise Resource Planning (ERP) system, which creates production WOs and houses associated data, such as workflows and operational standard hours, to pull work through a factory with results similar to that of POLCA. 



    Read more
  • Production Priority-setting Examples +

        There are numerous methods of setting priorities in a production environment, too numerous to discuss in total in this paper, but some of the more prevalent methods are discussed below.



    Read more
  • First Authorized - First Processed Work Flow +

        When looking at work flow through a factory from the perspective of minimizing cycle time and honoring demand-pull policies, work should be processed on a first authorized, first processed (FAFP) basis. In other words, once a WO has been authorized within a WC’s queue, it should be pulled into production on a FAFP basis.  Deviating from this policy can result in an increase in the average cycle time, unless batching of WOs will reduce their aggregate cycle times due to machine capacity.  For an example of the latter situation, a machine may be capable of simultaneously processing ten pieces, and if there are two five-piece (or fewer) WOs, they could both be processed at the same time to reduce their aggregate cycle time, improve efficiency and maximize capacity.  



    Read more
  • Demand-Based Production from a Flow-Time Versus Need-Time Perspective +

    From a flow-time perspective, Work Orders should arrive in a Work Center's queue at precisely the time when they are needed to be worked on.  This minimizes both production cycle-time and inventory investment. The desired time for the next WO to arrive for processing is when the currently-authorized work in a WC and its upstream-adjacent (UA) WCs has been started into the WC and cleared the first operation in the WCs routing. This assumes that demand exists for the WO at the next downstream work cell.



    Read more
  • Examples of the Vortex Authorization Process +

    The examples set forth in the table below illustrate the WO authorization process resulting from the pull-test in different circumstances.  In all the examples, a set of WCs such as shown in the following Figure is used.  There are two WCs (WC 130 and WC 135) that feed into a third WC (WC 145) and the downstream WC (WC 145) is presumed to be healthy (reference the discussion of Work Center Performance Testing) so that the pull-testing for this WC is active. 



    Read more
  • Calculating Flow Time in a Work Center +

    Using Standard Labor/Machine Processing Hours
    In the case where all units in a WO are processed as a discrete set, the Flow Time of a WO in a WC is equal to the Standard Process Hours of the WO.



    Read more
  • Demand-Based Production from a Work-Volume Perspective +

    When looking at authorizing work in upstream stages of production, the traditional Kanban system establishes quantity buffers, or queues, at each WC. Then when the buffer quantity hits a minimum value (the Queue Policy), the Kanban card is returned to its originating WC for replenishment. 



    Read more
  • Table of Definitions +

    The following is a Table of Definitions for the articles describing the Vortex technology.



    Read more
  • An Optimum Queue Policy +

    The formulae from Demand-Based Production from a Flow-Time Versus Need-Time Perspective and Demand-Based Production from a Work-Volume Perspective can now be combined to solve for the Queue Policy (XN).



    Read more
  • An Automated Demand-Pull System Embodiment +

    The Figures below illustrate an embodiment of the demand-pull system, which can be implemented using a software system with a database.  In this embodiment, a .NET service bus and MSSQL database running on a networked Microsoft Windows server are connected via the local area network (LAN) to individual clients in the various WCs. 



    Read more
  • Comparison of Time-Based Demand-Pull versus POLCA +

    POLCA (Paired Overlapping Loops of Cards with Authorization) is a prior art system to produce solutions to the application addressed herein, that is, demand-based shop floor control in a high mix, or high variety, production environment. 



    Read more
  • Vortex Shop Floor Control for Discrete Manufacturing +

    Is your manufacturing environment order-driven? Do you Engineer-to-Order or Customize-to-Order? Do your spaghetti diagrams look more like a network than continuous flow? If you struggle with production cycle-times that are too long and inventories that are too high, we have a solution!


    Introducing Vortex, a Shop Floor Control system designed to minimize your production cycle time and reduce inventory. Vortex works to pull production through your factory exactly when it’s needed! It predicts when a work center will be in need of more work, identifies the highest priority batch in all upstream work centers, and then authorizes the batch to be started just at the right time for it to reach the work center exactly when it is needed.


    Upstream work is only released if there is downstream demand, thus implementing one of the basic tenets of Lean Manufacturing – demand-pull production – in the high-variety, order-driven factory.


    Sounds simple, right?  In theory, yes.  However, if you’re talking dozens of work centers, dozens of different work flows and varying batches of sizes and flow times – predicting the time at which more work than is currently authorized for production will be needed can very quickly get complicated – the real-time calculations piling up pretty fast.

     
    Vortex streamlines the thousands of computations with a patent-pending algorithm, which works not only to synthesize all the math, but also integrate those solutions directly into your production system.


    Vortex’s modern, standards-based API is compatible with most ERP and Shop Floor Control systems.  The fully featured API allows your ERP and other internal systems to always stay up-to-date with the status of work on the shop floor. Vortex relies on your existing ERP system to create Work Orders according to your existing planning policies and inject them into the system through the API.  From there, Vortex handles the Starts into each work center based on demand-pull policies – minimizing both cycle-time and Work-in-Process inventories.  


    Check out our demo based on the following 5 products with individual work flows through 10 work centers. To view the demo, please click the link on this page - or drop us a line and we will take you for the tour.



    Read more